三角形は どんなふうにしたら 描けるの?
そぼくな ぎもん から スタートです
三角形が1つ描けたら 同じものを もうひとつ 描くことができます
三角形を1つ描くのに ひつようなものは 辺 と 角度ですね
1) 辺が1つ わかっているとき
1つの辺を 6cmとします 辺1つだけではでは 三角形は 描けませんね
あと なにが あったら 1つの三角形が 描けるでしょうか
そうです さらに 角度が 2つ あると 1つの三角形が 描けますね
6cmの1つの辺と 40° と 60° の2つの角度をもつ 三角形を 描いてみましょう
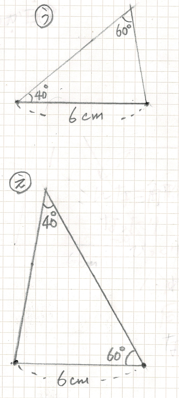
あ い う え の 4この三角形が 描けました
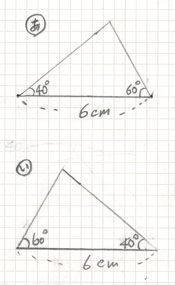
あ と い では 40°と 60°の 2つの 角は 6cmの辺の 両端の角 です
い は ひっくりかえして あ と かさね合わすと ぴったり 同じに なります
なので これは 1つの 三角形 と かんがえてよさそうです
う と え では 40° と60°の 角度は 6cmの辺の 両端の角ではないですね
う と え は かさね合わそうとしても 同じものに ならないですね
2つの角度が 1つの辺の両端の角でないときは 三角形は 2つできてしまい
1つに 決まらないことが わかります
三角形を描くとき 1つに決まる 描き方を すると 三角形の合同条件になります
この 場合 「1組の辺 と その 両端の角が それぞれ 等しい」と なります
かさね合わせると 同じものになる 2つの 三角形 は
合 同 同 で ある と いいます
2) 辺が 2つ わかっているときは どうでしょうか
3角形が 1つだけ 描ける 描き方 を みつけてみましょう
4cmと6cmの 2つの 辺 そして40°の 角 を もつ 三角形です
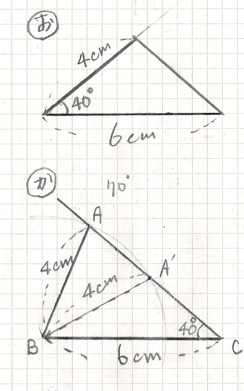
お は 40°の 角は 4cmと6cmの2つの辺の あいだ の 角に なっています
三角形は 1つに描けますね
か は 40°の 角は 4cmと6cmの2つの辺の あいだ の 角に なっていません
三角形は 1つに決まりませんね △ABCと △A’BC の 2こ 描けます
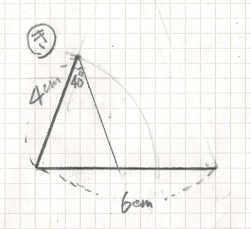
き も 40°の 角は 4cmと6cmの辺の あいだ の 角に なっていませんね
4cmと6cmの辺をもつ 三角形は 描くことが できません
2つの 辺 と 角度 が 1つ の ときは 2つの辺の あいだ の 角 で ないと
三角形は 1つに 決まらないことが わかります
3) 辺が 3つ わかっているときは 三角形は 1つだけ 描けます
この場合は 角度は なくても OKですね
図形と 証明 の 入口に ある 三角形の 合同条件は
三角形が 1つだけ 描ける 条件 (三角形の一意性)が 合同条件に なっていますね
