2つの角がひとしいことを 証明するとき 2つの角がふくまれる 三角形の合同を まず証明します
合同な図形では たいおうする角は ひとしいので 2つの角はひとしい というながれで証明します
角度 という ことば を 聞いたら わたしたちは 思いうかべます
対頂角
同位角
錯角
一直線上の角
外角
外角のせいしつ
ぐるり円の角
正三角形の1つの内角
ちょうちょ
ブーメラン
星
わたしたちは 思いうかべる力を もっています
そして なぜ? と 問いかける力 を もっています
対頂角は なぜ 等しいの? そぼくな 問いかけが とても たいせつです
なぜなら 1つ1つのそぼくな問いかけが わたしたちの 考えるちからを そだててくれるからです
ここでは 対頂角への そぼくな問いかけから
かさなり と いう 角度の見かた を身につけましょう
かさなり は 外角のせいしつ にも つながる 角度の見かたです
かさなり は ひとりで 二役を する 角度のことです
図を見てみましょう
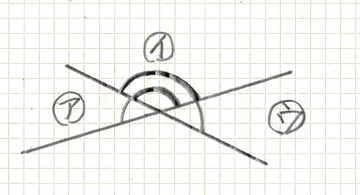
ア と ウ は 対頂角ですね 対頂角は ひとしい わけを かくにんしましょう
イ の 角 は 線が 2本で かさなっています これが かさなり です
イ の 角 は 一人二役 を しています
ア と いっしょに 一直線上の角 180° を つくります
ウ と いっしょに 一直線上の角 180° も つくります
ア + イ = 180 ①
ウ + イ = 180 ② です
① から ア = 180ーイ
② から ウ = 180ーイ
なので ア = イ と なり イ の 角 は 一人二役を しています
かさなり の もうひとつの 例を 見てみましょう
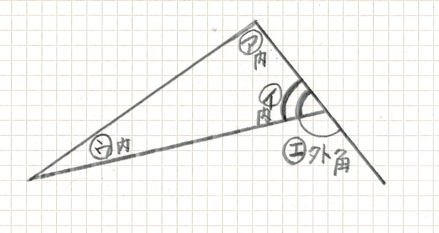
これは 三角形の 外角の せいしつ を あらわしています
イ の 角 が 線が 2本で かさなっていますね これが かさなり の 角です
イ の 角は ここでも 一人二役です
ア + ウ + イ = 180 ① 三角形の内角の和
外角 + イ = 180 ② 一直線上の角
①より ア + ウ = 180 ー イ
②より 外角 = 180 ー イ
なので 外角 = ア + ウ です
3年で学習する 三平方の定理 の 証明にも かさなり が 使われることがあります
正三角形 正方形 が からんでくる 証明問題に であったとき さんこうに
してみてくださいね
