円の面積をもとめる 計算は x3.14で 気持ちがなえそうです
x3.14を 2回 しないといけない 場合は もう かんべんしてくれ! と いった
気持ちですね
私たちの 先人たちは こんな場合でも ちゃんと 考えてくれています
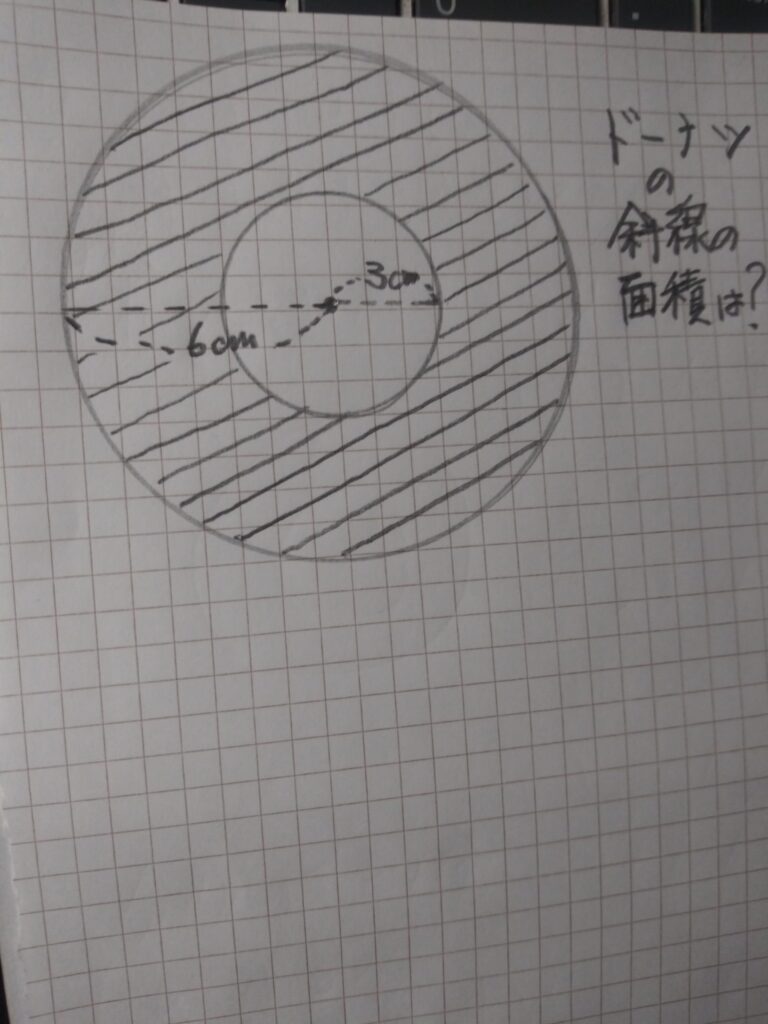
半径6cmの円の中に 半径3cmの円が あります
2つの円で できる ドーナツのかたちの 部分の 面積を もとめてみましょう
半径6cmの円の面積は 6x6x3.14
半径3cmの円の面積は 3x3x3.14
大きい円の面積 から 小さい円の面積を引くと いいですね
6x6x3.14-3x3x3.14 です
x3.14 の けいさんを 1回だけに します
x3.14を ひっぱりだします
あとに のこるのは 6x6-3x3 です
これに( )をつけて x3.14を つけます
(6x6-3x3)x3.14 です
(36-9)x3.14 なので 25x3.14
こうすると x3.14の けいさん は 1回で すみます
つまり 6x6x3.14-3x3x3.14 は (6x6-3x3)x3.14 で 言いかえることが できます
分配のきまりです
分配 と いうのは 私たちが ひっ算で かけ算をするとき いつも やっていることです
小3 の ころ から ずっと やっていますね
12x3
12
x 3
3を 2と 1に それぞれ 分けて 配るように かけますね これが 分配です
分配の きまり は けいさんの くふう で よく 使われます
これが 身につくと けいさんが とても 楽に なります
交かんの きまり 結合の きまり も けいさんの くふう で つかわれます
たとえば 25x 7x4 は
7と4を 交かんして 25x4x7 と しても OK です ( かけ算だけの式だから)
25x4x7 25x4 は 100だと ひらめいたら
かっこ を つけて
(25x4)x7 と します これで 25と4が むすばれました 先に けいさんしてね
という 意味です
すると100x7 で 答えは 700と なります
なれると 暗算できます
一度習った 分配の きまり を もし 忘れていたら ぜひ しっかり 回収(リトリーブ)しましょう
ゴールデン・レトリーバーの ように
分配のきまりの 感覚は 中3の 因数分解へと つながっていきます